Rotom’s Pokédex
|
#758 Salazzle |
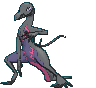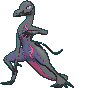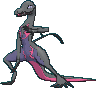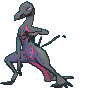
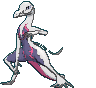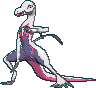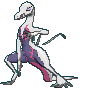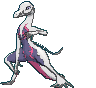
| | 1.2 m
(3'11") —
22.2 kg
(48.9 lbs.) |
|
 |
Toxic Lizard Pokémon |
|
|
|
Ability #1
• Corrosion - The Pokémon can poison the target even if it’s
a Steel or Poison type. Hidden Ability
• Oblivious - The Pokémon is oblivious, and that keeps it from
being infatuated or falling for taunts. |
AlolanDex
#162 Su Mo ~ #196 Ultra |
#758 Salazzle
• Evolution
#758 Salazzle
• Type efficacy
(Move Power × [4 | 2 | 1 |
0.5 | 0.25 | 0])
|
|
Normal |
Fighting |
Flying |
Poison |
Ground |
Rock |
Bug |
Ghost |
Steel |
Fire |
Water |
Grass |
Electric |
Psychic |
Ice |
Dragon |
Dark |
Fairy |
| 1 |
½ |
1 |
½ |
4 |
2 |
¼ |
1 |
½ |
½ |
2 |
¼ |
1 |
2 |
½ |
1 |
1 |
¼ |
| This table ignores the ability. |
#758 Salazzle
• Statistics, Effort values & Experience
(MIN–MAX: [0 IV, 0 EV, Nat.-10%] — [31 IV, 252 EV, Nat.+10%])
| |
HP |
Attack |
Defense |
Special Attack |
Special Defense |
Speed |
| Base Stats |
68 |
64 |
60 |
111 |
60 |
117 |
| Level 50 |
128-175 |
62-127 |
58-123 |
104-179 |
58-123 |
109-185 |
| Level 100 |
246-340 |
119-249 |
112-240 |
204-353 |
112-240 |
215-366 |
| Tot. Base Stats: 480 |
| Effort values (2) |
0 |
0 |
0 |
0 |
0 |
2 |
| Experience: 168 |
#758 Salazzle
• Pokédex Entries
| Sun | For some reason, only females have been found.
It creates a reverse harem of male Salandit that
it lives with. |
| Moon | Filled with pheromones, its poisonous gas can
be diluted to use in the production of
luscious perfumes. |
| Ultra Sun | Salazzle lives deep in caves and forces the
Salandit it has attracted with its pheromones
to serve it. |
| Ultra Moon | It punishes Salandit that couldn’t bring it food
with a fierce slap of its flame-spewing palm. |
#758 Salazzle
 Held item
Held item
#758 Salazzle
• Egg Groups
#758 Salazzle
• Moves, Learnset of Salazzle
By leveling up
Sun and Moon
| Move |
|
Power |
Accuracy |
PP |
Priority |
|
Normal |
-- |
100% |
20 |
0 |
| If any opposing Pokémon is the opposite gender of
the user, it is charmed, which harshly lowers its
Sp. Atk stat. |
|
Normal |
-- |
100% |
20 |
0 |
| If any opposing Pokémon is the opposite gender of
the user, it is charmed, which harshly lowers its
Sp. Atk stat. |
|
Normal |
-- |
100% |
20 |
0 |
| For four turns, this move prevents the target from
using the move it last used. |
|
Normal |
-- |
100% |
5 |
0 |
| The user compels the target to keep using the move
it encored for three turns. |
|
Dark |
-- |
100% |
15 |
0 |
| The user torments and enrages the target, making it
incapable of using the same move twice in a row. |
|
Normal |
-- |
85% |
15 |
0 |
| The user enrages and confuses the target. However,
this also sharply raises the target’s Attack stat. |
|
Normal |
40 |
100% |
35 |
0 |
| The target is physically pounded with a long tail, a
foreleg, or the like. |
|
Poison |
-- |
90% |
40 |
0 |
| A cloud of poison gas is sprayed in the face of
opposing Pokémon, poisoning those hit. |
|
Fire |
40 |
100% |
25 |
0 |
| The target is attacked with small flames. This may
also leave the target with a burn. |
|
Normal |
-- |
100% |
20 |
0 |
| A sweet scent that harshly lowers opposing
Pokémon’s evasiveness. |
|
Fire |
40 |
100% |
25 |
0 |
| The target is attacked with small flames. This may
also leave the target with a burn. |
|
Normal |
-- |
100% |
20 |
0 |
| A sweet scent that harshly lowers opposing
Pokémon’s evasiveness. |
|
Dragon |
-- |
100% |
10 |
0 |
| This attack hits the target with a shock wave of
pure rage. This attack always inflicts 40 HP damage. |
|
Poison |
30 |
70% |
20 |
0 |
| The target is attacked with a discharge of filthy
gases. This may also poison the target. |
|
Normal |
15 |
85% |
10 |
0 |
| The target is slapped repeatedly, back and forth,
two to five times in a row. |
|
Fire |
70 |
100% |
15 |
0 |
| The user attacks the target with a bursting flame.
The bursting flame damages Pokémon next to the
target as well. |
|
Poison |
-- |
90% |
10 |
0 |
| A move that leaves the target badly poisoned.
Its poison damage worsens every turn. |
|
Dark |
-- |
-- |
20 |
0 |
| The user stimulates its brain by thinking bad
thoughts. This sharply raises the user’s Sp. Atk stat. |
|
Poison |
65 |
100% |
10 |
0 |
| The user drenches the target in a special poisonous
liquid. This move’s power is doubled if the target
is poisoned. |
|
Fire |
90 |
100% |
15 |
0 |
| The target is scorched with an intense blast of fire.
This may also leave the target with a burn. |
|
Poison |
-- |
100% |
20 |
0 |
| Opposing Pokémon are drenched in an odd
poisonous liquid. This lowers the Attack, Sp. Atk, and
Speed stats of a poisoned target. |
|
Dragon |
85 |
100% |
10 |
0 |
| The target is attacked with a shock wave generated
by the user’s gaping mouth. |
By TM/HM
Sun and Moon
| Move |
|
Power |
Accuracy |
PP |
Priority |
|
Dragon |
80 |
100% |
15 |
0 |
| The user slashes the target with huge sharp claws. |
|
Poison |
-- |
90% |
10 |
0 |
| A move that leaves the target badly poisoned.
Its poison damage worsens every turn. |
|
Poison |
65 |
100% |
10 |
0 |
| The user drenches the target in a special poisonous
liquid. This move’s power is doubled if the target
is poisoned. |
|
Normal |
60 |
100% |
15 |
0 |
| A unique attack that varies in type depending on the
Pokémon using it. |
|
Dark |
-- |
100% |
20 |
0 |
| The target is taunted into a rage that allows it to use
only attack moves for three turns. |
|
Normal |
-- |
-- |
10 |
4 |
| Enables the user to evade all attacks. Its chance of
failing rises if it is used in succession. |
|
Normal |
-- |
100% |
20 |
0 |
| This full-power attack grows more powerful the
less the user likes its Trainer. |
|
Normal |
-- |
100% |
20 |
0 |
| This full-power attack grows more powerful the
more the user likes its Trainer. |
|
Bug |
80 |
100% |
10 |
0 |
| The user drains the target’s blood. The user’s HP is
restored by half the damage taken by the target. |
|
Normal |
-- |
-- |
15 |
0 |
| By moving rapidly, the user makes illusory copies of
itself to raise its evasiveness. |
|
Poison |
95 |
100% |
10 |
0 |
| The user strikes everything around it by swamping
the area with a giant sludge wave. This may also
poison those hit. |
|
Fire |
90 |
100% |
15 |
0 |
| The target is scorched with an intense blast of fire.
This may also leave the target with a burn. |
|
Poison |
90 |
100% |
10 |
0 |
| Unsanitary sludge is hurled at the target. This may
also poison the target. |
|
Fire |
110 |
85% |
5 |
0 |
| The target is attacked with an intense blast of
all-consuming fire. This may also leave the target
with a burn. |
|
Dark |
-- |
100% |
15 |
0 |
| The user torments and enrages the target, making it
incapable of using the same move twice in a row. |
|
Normal |
70 |
100% |
20 |
0 |
| This attack move doubles its power if the user is
poisoned, burned, or paralyzed. |
|
Fire |
50 |
100% |
20 |
0 |
| Cloaking itself in flame, the user attacks. Then,
building up more power, the user raises its
Speed stat. |
|
Psychic |
-- |
-- |
10 |
0 |
| The user goes to sleep for two turns. This fully
restores the user’s HP and heals any
status conditions. |
|
Normal |
-- |
100% |
15 |
0 |
| If it is the opposite gender of the user, the target
becomes infatuated and less likely to attack. |
|
Dark |
60 |
100% |
25 |
0 |
| The user attacks and steals the target’s held item
simultaneously. The user can’t steal anything if it
already holds an item. |
|
Normal |
60 |
100% |
15 |
0 |
| The user attacks the target with a song. Others can
join in the Round to increase the power of
the attack. |
|
Fire |
130 |
90% |
5 |
0 |
| The user attacks the target at full power. The
attack’s recoil harshly lowers the user’s Sp. Atk stat. |
|
Dark |
-- |
100% |
10 |
0 |
| The user flings its held item at the target to attack.
This move’s power and effects depend on the item. |
|
Fire |
-- |
85% |
15 |
0 |
| The user shoots a sinister, bluish-white flame at the
target to inflict a burn. |
|
Flying |
55 |
100% |
15 |
0 |
| The user nimbly strikes the target. If the user is not
holding an item, this attack inflicts massive damage. |
|
Ghost |
70 |
100% |
15 |
0 |
| The user slashes with a sharp claw made from
shadows. Critical hits land more easily. |
|
Dark |
50 |
100% |
10 |
0 |
| The user stores power, then attacks. If the user
moves after the target, this attack’s power will
be doubled. |
|
Dragon |
60 |
90% |
10 |
-6 |
| The target is knocked away, and a different Pokémon
is dragged out. In the wild, this ends a battle against
a single Pokémon. |
|
Poison |
80 |
100% |
20 |
0 |
| The target is stabbed with a tentacle or arm steeped
in poison. This may also poison the target. |
|
Normal |
-- |
85% |
15 |
0 |
| The user enrages and confuses the target. However,
this also sharply raises the target’s Attack stat. |
|
Normal |
-- |
-- |
10 |
0 |
| While it is asleep, the user randomly uses one of the
moves it knows. |
|
Normal |
-- |
-- |
10 |
0 |
| The user makes a copy of itself using some of its HP.
The copy serves as the user’s decoy. |
|
Normal |
-- |
-- |
20 |
0 |
| The user tells the target a secret, and the target
loses its ability to concentrate. This lowers
the target’s Sp. Atk stat. |
By leveling up
Ultra Sun and Ultra Moon
| Move |
|
Power |
Accuracy |
PP |
Priority |
|
Normal |
-- |
100% |
20 |
0 |
| If any opposing Pokémon is the opposite gender of
the user, it is charmed, which harshly lowers its
Sp. Atk stat. |
|
Normal |
-- |
100% |
20 |
0 |
| If any opposing Pokémon is the opposite gender of
the user, it is charmed, which harshly lowers its
Sp. Atk stat. |
|
Normal |
-- |
100% |
20 |
0 |
| For four turns, this move prevents the target from
using the move it last used. |
|
Normal |
-- |
100% |
5 |
0 |
| The user compels the target to keep using the move
it encored for three turns. |
|
Dark |
-- |
100% |
15 |
0 |
| The user torments and enrages the target, making it
incapable of using the same move twice in a row. |
|
Normal |
-- |
85% |
15 |
0 |
| The user enrages and confuses the target. However,
this also sharply raises the target’s Attack stat. |
|
Normal |
40 |
100% |
35 |
0 |
| The target is physically pounded with a long tail, a
foreleg, or the like. |
|
Poison |
-- |
90% |
40 |
0 |
| A cloud of poison gas is sprayed in the face of
opposing Pokémon, poisoning those hit. |
|
Fire |
40 |
100% |
25 |
0 |
| The target is attacked with small flames. This may
also leave the target with a burn. |
|
Normal |
-- |
100% |
20 |
0 |
| A sweet scent that harshly lowers opposing
Pokémon’s evasiveness. |
|
Fire |
40 |
100% |
25 |
0 |
| The target is attacked with small flames. This may
also leave the target with a burn. |
|
Normal |
-- |
100% |
20 |
0 |
| A sweet scent that harshly lowers opposing
Pokémon’s evasiveness. |
|
Dragon |
-- |
100% |
10 |
0 |
| This attack hits the target with a shock wave of
pure rage. This attack always inflicts 40 HP damage. |
|
Poison |
30 |
70% |
20 |
0 |
| The target is attacked with a discharge of filthy
gases. This may also poison the target. |
|
Normal |
15 |
85% |
10 |
0 |
| The target is slapped repeatedly, back and forth,
two to five times in a row. |
|
Fire |
70 |
100% |
15 |
0 |
| The user attacks the target with a bursting flame.
The bursting flame damages Pokémon next to the
target as well. |
|
Poison |
-- |
90% |
10 |
0 |
| A move that leaves the target badly poisoned.
Its poison damage worsens every turn. |
|
Dark |
-- |
-- |
20 |
0 |
| The user stimulates its brain by thinking bad
thoughts. This sharply raises the user’s Sp. Atk stat. |
|
Poison |
65 |
100% |
10 |
0 |
| The user drenches the target in a special poisonous
liquid. This move’s power is doubled if the target
is poisoned. |
|
Fire |
90 |
100% |
15 |
0 |
| The target is scorched with an intense blast of fire.
This may also leave the target with a burn. |
|
Poison |
-- |
100% |
20 |
0 |
| Opposing Pokémon are drenched in an odd
poisonous liquid. This lowers the Attack, Sp. Atk, and
Speed stats of a poisoned target. |
|
Dragon |
85 |
100% |
10 |
0 |
| The target is attacked with a shock wave generated
by the user’s gaping mouth. |
By TM/HM
Ultra Sun and Ultra Moon
| Move |
|
Power |
Accuracy |
PP |
Priority |
|
Dragon |
80 |
100% |
15 |
0 |
| The user slashes the target with huge sharp claws. |
|
Poison |
-- |
90% |
10 |
0 |
| A move that leaves the target badly poisoned.
Its poison damage worsens every turn. |
|
Poison |
65 |
100% |
10 |
0 |
| The user drenches the target in a special poisonous
liquid. This move’s power is doubled if the target
is poisoned. |
|
Normal |
60 |
100% |
15 |
0 |
| A unique attack that varies in type depending on the
Pokémon using it. |
|
Dark |
-- |
100% |
20 |
0 |
| The target is taunted into a rage that allows it to use
only attack moves for three turns. |
|
Normal |
-- |
-- |
10 |
4 |
| Enables the user to evade all attacks. Its chance of
failing rises if it is used in succession. |
|
Normal |
-- |
100% |
20 |
0 |
| This full-power attack grows more powerful the
less the user likes its Trainer. |
|
Normal |
-- |
100% |
20 |
0 |
| This full-power attack grows more powerful the
more the user likes its Trainer. |
|
Bug |
80 |
100% |
10 |
0 |
| The user drains the target’s blood. The user’s HP is
restored by half the damage taken by the target. |
|
Normal |
-- |
-- |
15 |
0 |
| By moving rapidly, the user makes illusory copies of
itself to raise its evasiveness. |
|
Poison |
95 |
100% |
10 |
0 |
| The user strikes everything around it by swamping
the area with a giant sludge wave. This may also
poison those hit. |
|
Fire |
90 |
100% |
15 |
0 |
| The target is scorched with an intense blast of fire.
This may also leave the target with a burn. |
|
Poison |
90 |
100% |
10 |
0 |
| Unsanitary sludge is hurled at the target. This may
also poison the target. |
|
Fire |
110 |
85% |
5 |
0 |
| The target is attacked with an intense blast of
all-consuming fire. This may also leave the target
with a burn. |
|
Dark |
-- |
100% |
15 |
0 |
| The user torments and enrages the target, making it
incapable of using the same move twice in a row. |
|
Normal |
70 |
100% |
20 |
0 |
| This attack move doubles its power if the user is
poisoned, burned, or paralyzed. |
|
Fire |
50 |
100% |
20 |
0 |
| Cloaking itself in flame, the user attacks. Then,
building up more power, the user raises its
Speed stat. |
|
Psychic |
-- |
-- |
10 |
0 |
| The user goes to sleep for two turns. This fully
restores the user’s HP and heals any
status conditions. |
|
Normal |
-- |
100% |
15 |
0 |
| If it is the opposite gender of the user, the target
becomes infatuated and less likely to attack. |
|
Dark |
60 |
100% |
25 |
0 |
| The user attacks and steals the target’s held item
simultaneously. The user can’t steal anything if it
already holds an item. |
|
Normal |
60 |
100% |
15 |
0 |
| The user attacks the target with a song. Others can
join in the Round to increase the power of
the attack. |
|
Fire |
130 |
90% |
5 |
0 |
| The user attacks the target at full power. The
attack’s recoil harshly lowers the user’s Sp. Atk stat. |
|
Dark |
-- |
100% |
10 |
0 |
| The user flings its held item at the target to attack.
This move’s power and effects depend on the item. |
|
Fire |
-- |
85% |
15 |
0 |
| The user shoots a sinister, bluish-white flame at the
target to inflict a burn. |
|
Flying |
55 |
100% |
15 |
0 |
| The user nimbly strikes the target. If the user is not
holding an item, this attack inflicts massive damage. |
|
Ghost |
70 |
100% |
15 |
0 |
| The user slashes with a sharp claw made from
shadows. Critical hits land more easily. |
|
Dark |
50 |
100% |
10 |
0 |
| The user stores power, then attacks. If the user
moves after the target, this attack’s power will
be doubled. |
|
Dragon |
60 |
90% |
10 |
-6 |
| The target is knocked away, and a different Pokémon
is dragged out. In the wild, this ends a battle against
a single Pokémon. |
|
Poison |
80 |
100% |
20 |
0 |
| The target is stabbed with a tentacle or arm steeped
in poison. This may also poison the target. |
|
Normal |
-- |
85% |
15 |
0 |
| The user enrages and confuses the target. However,
this also sharply raises the target’s Attack stat. |
|
Normal |
-- |
-- |
10 |
0 |
| While it is asleep, the user randomly uses one of the
moves it knows. |
|
Normal |
-- |
-- |
10 |
0 |
| The user makes a copy of itself using some of its HP.
The copy serves as the user’s decoy. |
|
Normal |
-- |
-- |
20 |
0 |
| The user tells the target a secret, and the target
loses its ability to concentrate. This lowers
the target’s Sp. Atk stat. |
#758 Salazzle
• Sprites & extra info…
|

